I love roguelikes. Traditional roguelikes. Turn based, grid based, punch-you-in-the-gut roguelikes.
The complexity, depth, and emergent gameplay in these games rival any other genre out there. The heavyweights like Nethack, Crawl, and ADOM can be played for years without mastering them… or sometimes without a single victory. And in the last decade, roguelikes have proven beyond all doubt how valuable their ideas are. Despite being a genre invented in 1980, new games are constantly borrowing roguelike ideas and even the name itself.

And yet we haven’t seen a big adoption of traditional roguelikes. Roguelite action has done gangbusters of course. Games such as Binding of Isaac sell millions of copies. Nuclear Throne and Spelunky aren’t too far behind. But where’s our Binding of Isaac? Where’s the turn-based dungeon crawler blowing up the Steam charts? Clearly, permadeath is something many gamers are willing to stomach. Games like Civilization are proof positive that they enjoy turn-based stuff too.
I’d argue that there’s nothing inherent in the structure of traditional roguelikes that is holding them back from mainstream success. It’s simply that, for the most part, the genre is still stuck in the 1980s. I’m not the only person that thinks that.
This series is about 4 pet peeves I have when it comes to roguelikes. They’re things that not only annoy the hell out of me, but that I suspect might be at the heart of why the genre lags behind. I’m going to give examples of games that either solve or exacerbate the problems and share my tiny attempt at improving things with my game Golden Krone Hotel.
Before we start it’s important to point out, you know, this is just like my opinion, man. Some of the things I hate are literally the very features other people love. I think that’s OK, considering the huge variety available in the genre.
Burden of Knowledge
It’s no fun playing a game without knowing the rules.
Sure, there’s something to be said for the joy of discovery. But when you’re playing to win, not knowing the rules and not understanding the mechanics fucking sucks.
Ever been introduced to a board game by a friend who knows the game well? Ever had that friend suddenly “remember” an obscure rule halfway through (right after they’ve taken advantage of the rule)? There’s nothing more frustrating!
Burden of Knowledge1 is when game rules are so opaque that they’re nearly impossible to learn by just playing the game. Instead, you have to spend time outside of the game learning how to play the game… assuming you can find the information you need at all.
DND vs MTG
I tried to get into Dungeons and Dragons in college and it just didn’t click for me. At the same time, I was playing a ton of Magic the Gathering. I later realized these games are polar opposites when it comes to learning. With each, you have to learn a few rules to get started of course. Later on, however, the way you learn diverges dramatically.
When someone needed to learn a spell or pick a feat in Dungeons and Dragons, they often stopped the game for 30 minutes to skim the player handbook and decide what to do. The basic rules of the game are over 100 pages! You have so many choices at any given moment of the game. The problem is that understanding all those choices requires a lot of reading.
Contrast with Magic the Gathering. Even though the game has a lot of depth, you only have to deal with a handful of choices on each turn. When your opponent plays a new card you’ve never seen, something magical happens. You read the words on the card and figure it out in seconds.

In comparison to tabletop games, videogames actually have it pretty easy. They can simulate entire worlds and have the player learn on the fly just by mashing keys and seeing the result. In theory, we should never have to read rules while playing a computer game. In practice though…
Spoil Story
If we’re talking about polar opposites in the roguelike world, I can’t think of a better pair than Nethack and Dungeon Crawl Stone Soup. Nethack is notorious for it’s reliance on spoilers. In Nethack, there are dozens of ways to instantly kill yourself. Conversely, if you know the right secrets you can use ridiculously powerful abilities for free (like preventing monsters from attacking you). My first experience with Nethack was trying and failing for 10 minutes to get out of the very first room because I couldn’t figure out how to open a door. Let’s just say I’m not a fan of this approach. If you are, more power to you.
 20+ ways to insta-die in Nethack
20+ ways to insta-die in Nethack
On the other hand, DCSS takes a stand against spoilers. Check out this tidbit in the “philosophy” section of the Crawl manual:
Things ought to work in an intuitive way. Crawl definitely is winnable without spoiler access. Concerning important but hidden details (i.e. facts subject to spoilers) our policy is this: the joy of discovering something spoily is nice, once. (And disappears before it can start if you feel you need to read spoilers – a legitimate feeling.) The joy of dealing with ever-changing, unexpected and challenging strategic and tactical situations that arise out of transparent rules, on the other hand, is nice again and again.
Amen.
It’s not that there are no surprises to discover in DCSS. There definitely are. The Abyss anyone??? Rather the surprises are discoverable simply by playing the game. If you play very carefully, you have a reasonable chance to deal with any surprises on the fly. Remember the plethora of instadeaths in Nethack? There’s only two kinds in Crawl: starvation and falling into water/lava. In both cases, the game gives you ample warning that things are about to go belly-up.
Burden of Knowledge goes way beyond cheap deaths and big spoilers. There are tons of things to learn. What does this monster do? What does that spell do? Where do these stairs lead? What options do I have available on this turn? The amount of material you have to figure out in a big roguelike must add up to a few college courses (which might explain a lot for some of us). And that doesn’t even cover all the basic stuff (like what red bars signify in games) we take for granted.
So how are we going teach players all that stuff? Here are some common techniques. I’ve ordered them by their proximity to the ideal method, actually playing the real game.
The 6 Circles of Roguelike Learning Hell
Tutorials
Tutorials are great for quickly learning the basics. On the plus side, you are playing the game… sort of. It’s a stilted, challenge-free, and dead end version of the game, but at least you’re playing that version instead of reading a wall of text.
Hints
Hints are like mini-tutorials. A minimal amount of text presented in-game at exactly the right time you need the information. You do have to read, but you do so right in the middle of playing. Hints should be made unobtrusive as possible, preferably with an option to turn them off completely.
Modal hints force the player to read them, but are sometimes needed to convey crucial information.
Tooltips & Descriptions
The third circle isn’t that bad: on-demand information delivered in game that (hopefully) obscures very little of the screen. Tooltips help you quickly learn the UI. Good descriptions greatly reduce Burden of Knowledge regarding mechanics. It’s particularly useful when monster descriptions tell you what kind of spells, resistances, and attacks to expect.
Message log
Messages logs are a weird holdover from text adventures. Most modern games have too much going on too fast to even support a log, but the pace in roguelikes sort of allows them to work. A message log is a safety net for understanding. If the game fails to explain something visually, it can always go in the log and you don’t even have to stop playing to read it.
The utility of the message log is what makes it so dangerous. It’s very tempting to just dump stuff in the log instead of doing the very hard work of making it clear what’s happening on the play field. Even worse is that the log explains events after they happen. For small effects, that’s alright. For instadeaths, it doesn’t tell you anything until the game is over and you’ve potentially lost 20 hours of your life.
Help menus & manuals
To a first approximation, nobody reads help menus. As a designer, you absolutely cannot expect people to do it. Hopefully, the pattern is clear enough: the further removed from the game you are, the less enjoyable the learning and less likely someone is to seek out the information. In some sense the help menu is in the game, but you’re definitely not playing while you read it.
Wikis & guides
Abandon hope all ye who enter here. Because if you alt-tabbed over to a wiki, you have indeed given up on all hope of the game teaching you how to play.
Don’t get me wrong. On many occasions, I’ve been grateful for detailed wikis. But that’s really only after the game has hooked me for good. If I try out a new game and get stumped, I’d rather dump it than go read an essay about the difference between Flails and Polearms. Now consider your average steam user who has no idea what a roguelike is and stumbles across one.
Learning through level design
The above techniques are not all bad. If all roguelikes had good tutorials, hints, and tooltips, the genre would be dramatically more welcoming for beginners. I’ve added these things to Golden Krone Hotel and the game has clearly benefited. I have tooltips on every single button and UI element, detailed descriptions, a small hint system, and I developed a pretty neat little tutorial.
Still, I can’t help but feel we could do a lot better.
Let me hand it off to this Sequelitis video, which explains things so much better than I can:
Also check out How I Got My Mom to Play Through Plants vs. Zombies. This video by the designer of PvZ is a masterclass in teaching new concepts to players. The learning curve in PvZ is so damn good that, when development was completed, they completely replaced the Help menu with a joke:

Anyway, the theme of these two videos is that games shouldn’t have separate tutorials. People don’t like to read and they really don’t like to be forced to learn. In my experience, many players would rather struggle for hours not understanding stuff than spend 10 minutes in a boring tutorial.
Instead a game should present the player with a series of challenges with increasing difficulty such that an “aha moment” is inevitable long before the real difficulty comes.
I actually tried this with early versions of Golden Krone Hotel. You would encounter a high level foe in a narrow hallway at the start of every game. The only way to advance was by exploiting the main mechanic, killing vampires with sunlight. It did work as a teaching tool and it made people feel very clever. But it also forced experienced players to waste time whenever they started a new run and it sacrificed part of the procedural generation on the first floor. I removed this inline tutorial years ago and never thought much about it.

After recently watching the above videos, however, I was desperate to once again incorporate a “blended tutorial” into my game. It’s not an easy goal to accomplish within the context of a roguelike. You don’t want to bore the player by forcing them to repeat the same content again and again. I was stumped until I thought back to the most polished roguelike I’ve ever played and it hit me…
QUD vs SPROG
Yet again we have two polar opposite roguelikes, Caves of Qud and Sproggiwood. These wildly different games are in fact made by the same developer, Freehold Games!
Caves of Qud
I love this game so much, but the user interface is a nightmare for beginners. Chalk it up to a short attention span or a lack of patience, but I’ve had a very hard time getting into the game. The help menus are good and a “Ten Things You Should Do When You Start To Play” section is nice, but playing the game itself can be quite bewildering.
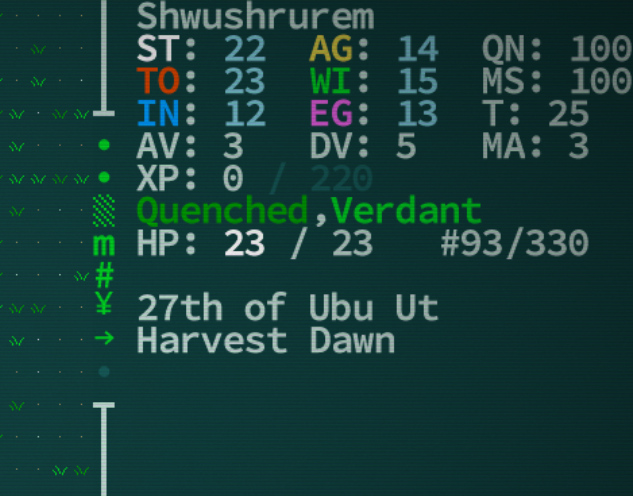
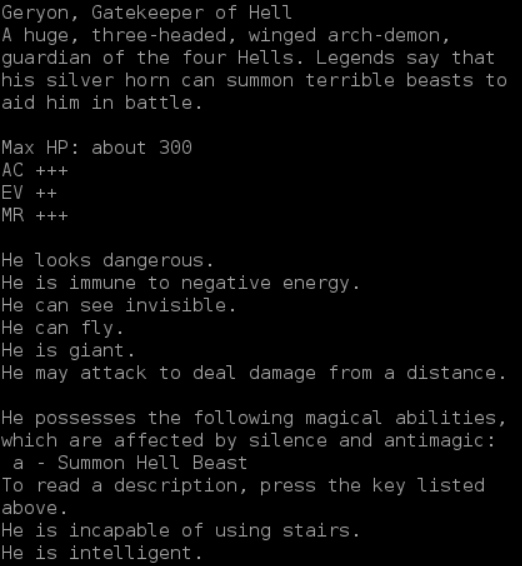
When you start up Caves of Qud, this is the sidebar staring you in the face. There’s over a dozen incomprehensible stats. As far as I know, there are no tooltips to explain them. If some of these numbers get big, you’re in real trouble (my favorite being T for Temperature). There’s also a bunch of cryptic symbols on the left. Even words like Verdant confuse me. Qud make Jeremiah feel dumb.
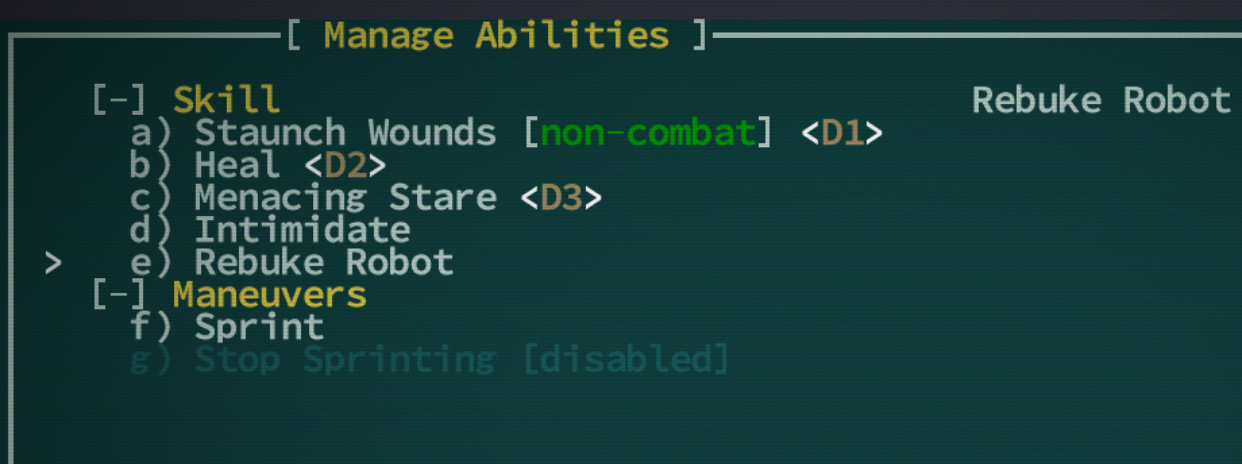
Here’s the Abilities menu. First, recognize that a new player doesn’t even know this is a thing they can get to. Once there, you’ve got to manually bind all of your abilities. Meanwhile, you don’t get a description of exactly how the abilities work. I guess they were explained during character creation, but I often roll a random character and don’t see that.
To be fair, it does seem that Qud’s UI is slowly improving and there’s a lot more coming on the roadmap.
Sproggiwood
Sproggiwood on the other hand has a beautiful interface.
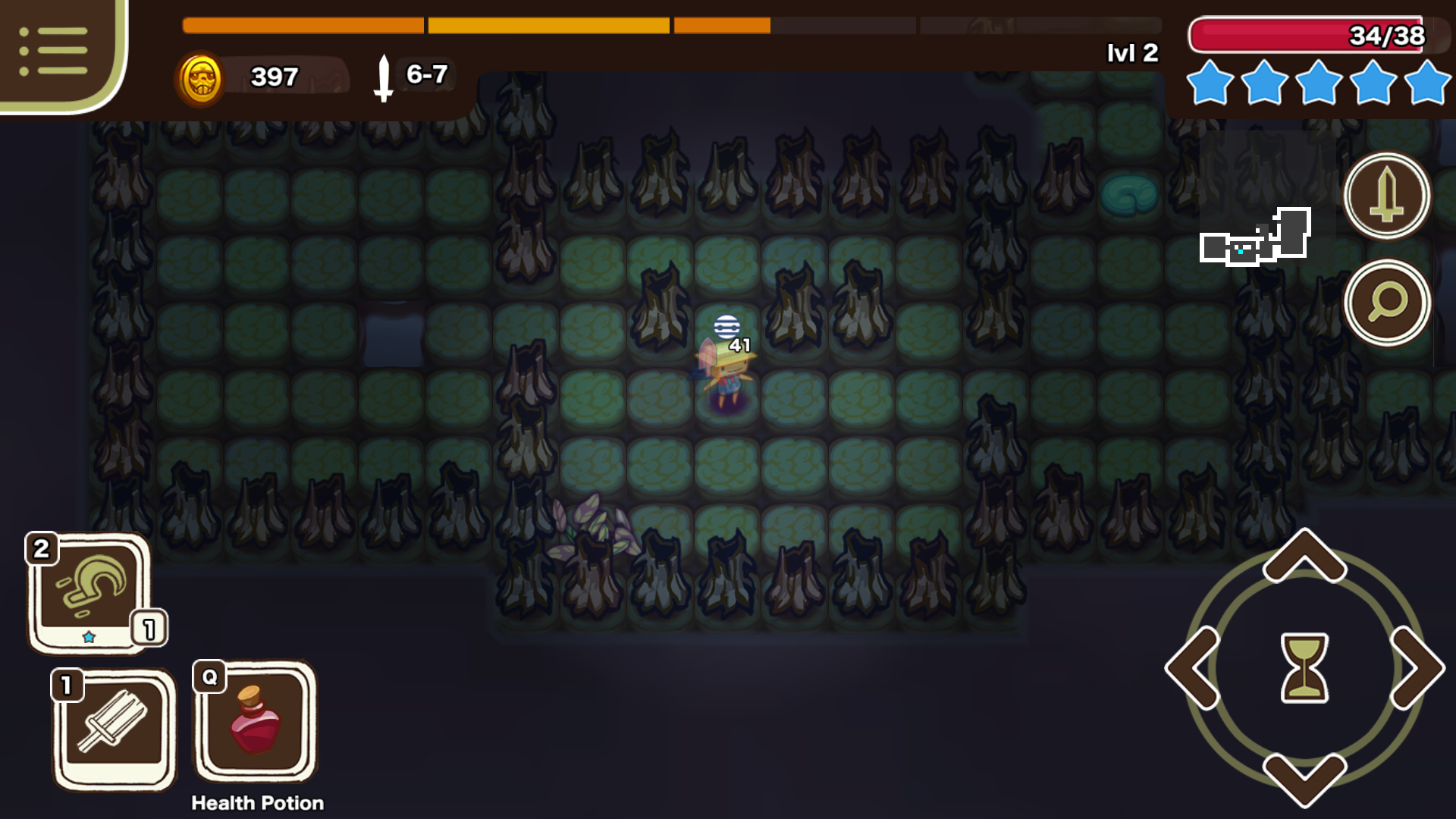
- Every possible action you can perform (including wait!) is on screen somewhere
- A magnifying glass icon lets you examine any of your abilities
- Despite seeming rather sparse, a good deal of information is represented: the minimap, the duration of the character’s invisibility, XP, and the level/cost of each ability.
- There are keypress hints on every button (more on this later)
Sproggiwood also has a delightful tutorial. This is how it should be done. Mandatory, but short. Not even labeled a tutorial. Valuable on it’s own and not a slog (the tutorial is very funny).
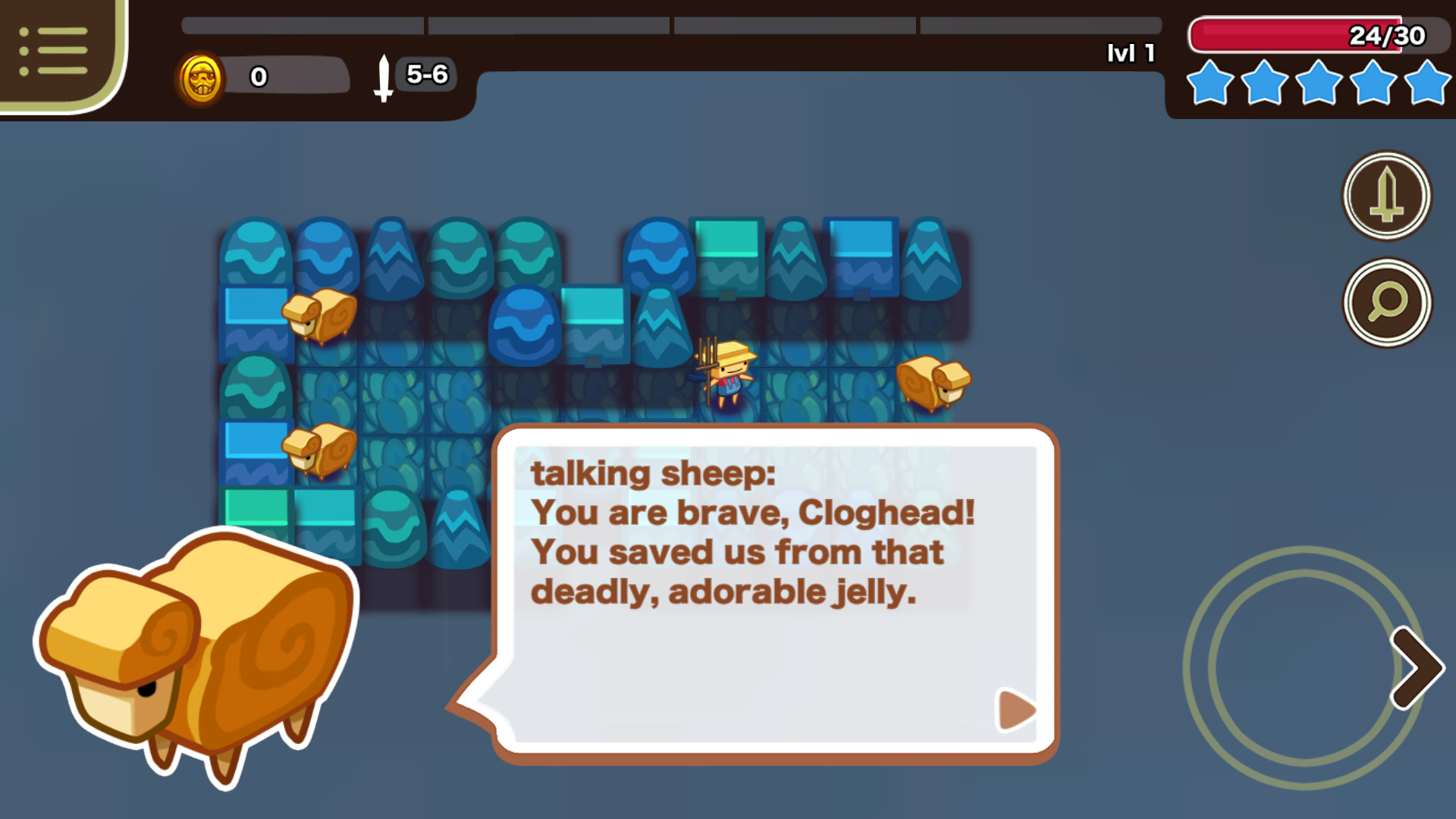
So Sproggiwood helped me figure out what to do: jam the tutorial right on the start of my game. When the tutorial is over, it jumps straight into the regular game and when the player dies, the next run skips right over the tutorial.
Which is better?
Obviously, it’s easier to make a simpler UI if the game is simpler. It’s easier to reduce Burden of Knowledge if there’s simply less to learn. Sproggiwood fits this description, but so do many of my favorite roguelikes: 868-HACK, Hoplite, and Auro. And to some extent, so does my game.
But my point isn’t to only make simpler games. Caves of Qud, even with all its flaws, seems like the more successful game because of its complex systems. Just check the Steam reviews: 85% positive for Sproggiwood vs 99% positive of Caves of Qud. My point is let’s strive for the best of both worlds. Games as deep as Qud, but as easy to learn as Sprog. That’s not an easy task, not at all. But the payoff could be huge.
If you want to see how well I accomplished my goal of reducing Burden of Knowledge, check out the latest update to Golden Krone Hotel. And join us next time when we talk about Identification systems.
[1] As far as I know, the term Burden of Knowledge was popularized by designers at Riot Games. All in all, that’s pretty hilarious considering League of Legends is a game with about 700 abilities, of which a great portion are indicated by similar glowing/flashing effects.

19 replies on “Things I Hate About Roguelikes – Part 1: Burden of Knowledge”
100% disagree with point 1. I enjoy the part of learning a game’s hidden ruleset more than any other mechanical aspect of a game. One might posit that all mechanical aspects of a game are a learning process. I think the popularity of the Dark Souls games is proof that I am not alone in this.
I enjoyed aspects of Dark Souls, but consider the intentionally obscure mechanics to be an affront to the player. Putting in unknowable calculations that the playerbase can’t figure out for months until they *read the fricking code* seems like a waste of the player’s time: https://waypoint.vice.com/en_us/article/the-long-desperate-search-to-understand-poise-in-dark-souls-3
I would probably have appreciated this kind of stuff when I was younger, but as is I’m usually very short on time when it comes to gaming. And I don’t want to waste a lot of time figuring things out.
Some games are specifically designed around discovery. You could include Dark Souls in there, but I’m specifically thinking of games like The Witness or Starseed Pilgrim. If that’s the main idea, I’m fine with it.
In any case, you are certainly not alone. As I tried to emphasize in this post, different strokes for different folks.
Sure. My point is learning in the game is fine. Learning outside the game blows. Spending 20 hours to learn one thing is awful too.
Which mechanical aspects of dark souls are a learning process? To me, as someone who has obsessed over the souls series since demon’s, I don’t understand that claim at all. It looks like the souls games present every single action your character can do clearly and at the start of the game. Everything you pick up from then on tells you what it is. Items have descriptions that let you know their effect, and gear has attribute modifiers that show you how it impacts you. Everything in a souls game is fair and balanced, you can blame yourself for every single death. It’s brutal and unforgiving, but in no way is it unfair. Getting better at souls games is a skill building process, not a learning process. I’d love to hear if you have examples of the contrary though
I linked to an example in the comment above: https://www.vice.com/en/article/bnjpm3/the-long-desperate-search-to-understand-poise-in-dark-souls-3
In the first Dark Souls, it seems like there are a lot of examples of incorrect or misleading item descriptions. https://gamefaqs.gamespot.com/boards/606312-dark-souls/68150528
Great read and refreshing to meet another developer with similar mindset on tutorials. What is the game you working on? Are you on TIGsource by chance?
Thanks. It’s a traditional roguelike about killing vampires called Golden Krone Hotel.
I am indeed on TIG. Here is my devlog: https://forums.tigsource.com/index.php?topic=50482.0
I disagree than in MtG “You read the words on the card and figure it out in seconds.”.
First — there are lots of rules to learn first, to understand the basic mana/fighting system and to understand the various special words such as vigilance or haste. “The Comprehensive Rules are available from Wizards of the Coast in TXT, PDF, and DOCX formats, and are 210 pages long.”
Second — while “Defender” was explained in your example card, this is not always the case, e.g. Dirgur Nemesis “Defender, Megamorph 6colorless+1blue” (defender is not explained, megamorph is explained but if you don’t know this mechanics you won’t understand what happened if your opponent has used it), Ojutai Exemplars: “Ojutai Exemplars gains first strike and lifelink until end of turn” (“lifelink” is usually explained because it is non-standard but not on this particular card, “first strike” is standard but still you must know it)
Third — it is difficult to make informed decisions if you do not know what cards your opponents might potentially have (e.g., a card may be stronger than it appears because of some combo).
I think e.g. Dominion is much better in this regard — like in MtG rules are given by the cards themselves, but the general rules are quite easy (fixing the first point), you usually see all the cards in the game (fixing the third point) and if cards with additional rules appear, they can be safely explained before the game (lessening the second point).
It looks like I’ve made a surprisingly controversial point. Hmm. I had this similar argument with someone on reddit and the 224 page rule book came up there too. As I pointed out there, these are two games owned by the same company and the “Basic Rules” for MTG are 15 pages while the “Basic Rules” for D&D are 110. The comprehensive rules are reference material only.
I would definitely agree that Magic is not the perfect example or the most learnable game. Card/board games with a finite and small set of cards are much easier. But actually the potentially infinite breadth of MTG combined with the ability to learn things on the fly is what makes it interesting to me.
It’s definitely true there are rules that are not explained on all cards (defender, deathtouch, etc.), but those are things explained in a short 3 page glossary on the 15 page basic rulebook.
I’m not making that argument at all. I don’t think roguelikes or any other game have a responsibility to teach you everything about all the content up front or to teach you all the strategies either.
Perhaps my experience of MTG just differs from everyone else’s and it wasn’t a good example. Thanks for the comment, though!
old MTG cards didn’t have Vigilance or Haste; if there was a card that had some of those effects, those were explained in the card (eventually they put those effects names, so more text could be fitted in)
You don’t need to read anything at all to play DnD unless you’re the dungeon master. You role play. You sit there and tell the Dungeon Master what you want to do and he can guide you. You can pick up everything you need just from the conversation at the roleplaying session and before and after it.
Plus a lot of us roleplayers actually love to read manuals anyway. Some people read the manuals and get immersed in the worlds and never even play the game. We like reading.
In fact DnD is in a way a much more approachable game than MtG because you don’t have to buy a ton of stuff if you’re not DMing: a set of dice and that’s it. MtG is going to cost you a ton, isn’t it? And it’s ongoing.
This is something I didn’t mention in the post, but when I was playing the GM wasn’t experienced. If there was some confusion about the rules, we *all* had to sit around waiting on one person to read them.
I don’t disagree that MTG has huge problems with monetary barriers and the ongoing expansions is ridiculous. But my friends and I used to buy 1000 packs of cards and draft from them for $10. Didn’t seem like a huge burden if you were willing to play older stuff.
[…] This is a 4 part series on annoyances I have with roguelikes. Last time we covered Burden of Knowledge. […]
I strongly agree with the premise, but disagree with some of the examples.
Spriggiwood is actually quite bad as far as burden of knowledge goes. There’s a TON of missing information and it’s entirely unclear how many things (e.g. several abilities) actually work from their vague descriptions. It’s certainly far easier to play the game at a basic level, but you’re still not able to make actual informed decisions.
Meanwhile, Isaac has a ridiculous knowledge barrier and is popular despite this, so doesn’t make for a great example there either =) It’s chock full of vague descriptions and outright lies. “Damage Up” can mean +0.3 damage (which is then further obfuscated through a weird formula), or it can mean you get a 50% damage multiplier and about a dozen other things.
Anything that tries to push designers to actually friggin’ EXPLAIN WHAT ANYTHING DOES inside the game is great by me, though, so keep preaching. Something like 4 out of 5 new games I try features blatantly missing information, and probably half feature outright lies (e.g. ‘90%’ chance to hit is actually ‘100%’ in Darkest Dungeon).
Sproggiwood’s descriptions are not spectacular, true, especially for monsters. I could rage over the cute description on Happy Fish Mate despite it being one of the most annoying enemies of all time.
I’m really only pushing for roguelikes to explain things at a basic level, which they don’t all currently do. More detail is great, but it’s a hard problem to explain so much. Outright lies are unacceptable (I’m thinking Dark Souls). The example in Darkest Dungeon makes a bit of sense though because players assume 90% basically means guaranteed anyway.
Thanks for the comment!
I like Angband as a counter-example to Nethack. According to David Craddock’s book, this was actually one of the founding design decisions in Angband – to craft a roguelike where everything you need to know can be learnt through gameplay alone. I don’t think it succeeds perfectly (some stats aren’t very clear) but I applaud the attempt. Nethack has interesting ideas but the opacity of it is very offputting.
I did not know that. Very interesting. All I had heard about Angband is that it’s insanely hard, so that’s somewhat surprising. It makes sense that even during Nethack’s time, there would have been some pushback against its design.
[…] achieving mastery and learning to avoid the many sadistic and brutal ways games like Nethack will insta-kill you. Learning controls, at least enough to be able to move around and perform common actions, is table […]
[…] This is a 4 part series on annoyances I have with roguelikes. Last time we covered Burden of Knowledge. […]
I couldn’t agree more about the Burden of Knowledge problem. It’s why I have only an academic interest in ever trying Nethack.
In my own roguelike, Caverns of Xaskazien II, everything is tooltipped. Point your cursor at a monster – here’s 100% of its stats, your odds to hit, your damage ranges, its odds to hit, its damage ranges, etc. Wonder what a wand does? Point at it. 100% of all information is provided – what it does, how many charges it has, the odds it will take effect. The same goes for every item, every spell, every miracle, every npc, every terrain feature, every attribute, perk, skill. Even pointing at your character’s name tells you something of use.
I’d like to add a tutorial one day, but am reticent as the game continues to evolve, in case it becomes obsolete. Of course, the game’s been evolving for 25 years, so I gotta take the plunge some time.
Enjoying this read. On to the next!